Hello everyone, in this article I want to share you about how to calculate triangle are using heron’s formula with python.
I’m just getting interested in Python and how it can be combined with math.
When I was learning math in elementary school, we mainly calculated the area of triangles using a formula
But today, I’m going to try implementing this using Python.
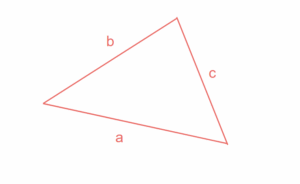
Observe the illustration above, which uses a scalene triangle.
Usually, to calculate the area of a triangle, we use the known base and height.
When you’re solving triangles that don’t have a right angle or equal sides like a scalene triangle the basic area formulas won’t work.
To calculate an area of scalene triangle we can using this Heron’s formula:
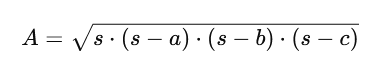
s = semi-perimeter (half the sum of all its sides)
We can use the following to calculate the semi-perimeter:
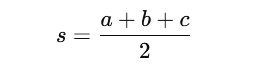
That’s where Heron’s Formula comes in handy.
In this article, we’ll explore how to apply it and implement it using Python.
Let’s start with something simple
I started by simply entering the lengths of the three sides of the triangle.
First, you input the lengths of the three sides.
Second, calculate the semi-perimeter, then use Heron’s formula to find the area of the triangle.
After that, we can display the triangle’s area in the terminal.
# ----------------------------------------
# Calculate Triangle using Heron`s Formula
# ----------------------------------------
import math
# Read the lengths of the three sides of the triangle
a = float(input("Enter length of side a: "))
b = float(input("Enter length of side b: "))
c = float(input("Enter length of side c: "))
# Store the sides in a list
sides = [a, b, c]
# Calculate the semi-perimeter (half the sum of all sides)
s = sum(sides) / 2
# Calculate using Heron`s formula
area = math.sqrt(s * (s - a) * (s - b) * (s - c))
# Print the area of the triangle
print("-----------------------------------")
print("Area of the triangle is:", area)Let’s try it.
$ python main.py
Enter length of side a: 10
Enter length of side b: 10
Enter length of side c: 10
-----------------------------------
Area of the triangle is 43.30If all the lengths are set to 10, the area of the triangle will be 43.30.
Perfect! It works!
Let’s make it with the function
I think, we need to wrapping into function to calculate the triangle.
I believe, an edge case occurs when the sides of the triangle are set to 30, 5, and 2.
That’s not valid length to make a triangle.
So, I added new function that called is_valid_triangle to check the lengths of a triangle. It will return boolean value.
Only valid triangles that will be calculated in this code.
# ----------------------------------------
# Calculate Triangle using Heron`s Formula
# ----------------------------------------
import math
def calculate_area(a, b, c):
"""Calculate the area of a triangle using Heron's formula."""
s = (a + b + c) / 2
return math.sqrt(s * (s - a) * (s - b) * (s - c))
def is_valid_triangle(a, b, c):
"""Check if the sides can form a valid triangle."""
return a + b > c and a + c > b and b + c > a
# Read the lengths of the three sides of the triangle
a = float(input("Enter length of side a: "))
b = float(input("Enter length of side b: "))
c = float(input("Enter length of side c: "))
print("-----------------------------------")
# Check if the sides form a valid triangle
if is_valid_triangle(a, b, c):
# Calculate the area of the triangle
area = calculate_area(a, b, c)
# print area of the triangle
print(f"Area of the triangle is {area:.2f}")
else:
# print error message if the triangle is invalid
print("The lengths provided do not form a valid triangle")
Let’s try it!
It’s not a valid triangle.
$ python main.py
Enter length of side a: 30
Enter length of side b: 5
Enter length of side c: 2
-----------------------------------
The lengths provided do not form a valid triangleIt’s a valid triangle.
$ python main.py
Enter length of side a: 6
Enter length of side b: 8
Enter length of side c: 10
-----------------------------------
Area of the triangle is 24.00How to solve with Python OOP
I refactored the code using a class-based object-oriented programming approach
Sometimes, using OOP makes your code cleaner and easier to manage.
Especially when you’re working with things that naturally map to real-world objects, like triangles in geometry.
I created the is_valid method to validate the triangle and the area method to calculate its area.
# ----------------------------------------
# Calculate Triangle using Heron`s Formula
# ----------------------------------------
import math
class Triangle:
def __init__(self, a, b, c):
"""Initialize the triangle with sides lengths."""
self.a = a
self.b = b
self.c = c
def is_valid(self):
"""Check if the sides can form a valid triangle."""
return (
self.a + self.b > self.c and
self.a + self.c > self.b and
self.b + self.c > self.a
)
def area(self):
"""Calculate the area of the triangle using Heron's formula."""
s = (self.a + self.b + self.c) / 2
return math.sqrt(s * (s - self.a) * (s - self.b) * (s - self.c))
def main():
# Read the lengths of the three sides of the triangle
a = float(input("Enter length of side a: "))
b = float(input("Enter length of side b: "))
c = float(input("Enter length of side c: "))
print("-----------------------------------")
# Create a Triangle object
triangle = Triangle(a, b, c)
# Check if the triangle is valid by calling the is_valid method
if triangle.is_valid():
# Calculate the area of the triangle by calling the area method
area = triangle.area()
# Print area of the triangle
print(f"Area of the triangle is {area:.2f}")
else:
# Print error message if the triangle is invalid
print("The lengths provided do not form a valid triangle")
if __name__ == "__main__":
main()
Let’s try it.
$ python main.py
Enter length of side a: 5
Enter length of side b: 12
Enter length of side c: 13
-----------------------------------
Area of the triangle is 30.00If not a valid triangle.
$ python main.py
Enter length of side a: 3
Enter length of side b: 56
Enter length of side c: 34
-----------------------------------
The lengths provided do not form a valid triangleGreat! That’s perfect!
Conclusion
Calculating area of triange using Heron’s formula is powerful when only the side length are known.
And when combined with Python, it becomes not only practical but also fun to implement! 😀
We can also use the easiest way, using a Python function, up to using an OOP (Object-Oriented Programming) approach.
If you have other ideas or alternative methods, feel free to share them in the comments below.
Happy coding!